Come abbiamo rimarcato in precedenti occasioni, l’applicazione di tecniche di Gann comporta soprattutto un problema di scala.
Questo significa che spesso non è possibile applicare direttamente questi metodi in base ai valori dell’asset che abbiamo scelto.
Potrebbe talora essere necessario modificarli, in base ad opportuni coefficienti.
Nel precedente articolo abbiamo visto come dividere i valori troppo grandi, per avere dei quadrati di minimo e di massimo gestibili.
Oggi vediamo la costruzione inversa rispetto ai quadrati di minimo e di massimo.
Potrebbe infatti capitare che vi siano valori così bassi, relativi alle quotazioni di un asset, che non è possibile applicarli direttamente nella costruzione di determinate tecniche di Gann, come nel caso di quotazioni troppo elevate.
Un esempio è offerto dal cross euro dollaro.
I quadrati di minimo e di massimo: costruzione inversa
Proviamo, ad esempio, a costruire un quadrato di minimo in base ai valori desumibili da un rilevante bottom dell’euro dollaro.
Si tratta del minimo a 0,8229, raggiunto ad agosto 2000.
Volendo costruire un quadrato di minimo, su time frame mensile, dovremmo considerare un quadrato avente un numero di unità temporali addirittura inferiore all’unità, ed una 1X1 pari ad 1.
Infatti 0,8229/0,8229 porta sempre ad 1.
Ma, utilizzando questi parametri, avremmo questo risultato grafico.
Come notiamo, il grafico si tradurrebbe solo in una serie di linee schiacciate, senza alcuna possibilità di utilizzo pratico.
Abbiamo detto come si risolve il problema, nel caso di quotazioni eccessivamente grandi.
In questo caso, ci troviamo invece a fronte di quotazioni troppo ridotte.
Ma possiamo risolvere il problema con un metodo inverso, rispetto a quello spiegato nel nostro precedente articolo.
Si considera il valore del bottom e lo si moltiplica per due, o per tre, e ogni risultato ottenuto, a sua volta, viene moltiplicato per due o per tre, secondo il coefficiente che abbiamo scelto.
Questo sarà il risultato da applicare al numero di unità temporali.
Quindi si divide questo risultato per il valore originario del bottom.
Infine, si divide il numero 1 per tale risultato, e questo sarà il valore della 1X1, da applicare al nostro quadrato,
Ancora una volta, più facile farlo che spiegarlo.
L’applicazione del metodo
Partiamo dal minimo di 0,8229 e moltiplichiamo per 3 un certo numero di volte consecutivamente.
Quindi: 0,8229X3X3X3X3X3, da cui otteniamo 199,96.
Questo sarà il numero di unità temporali del quadrato.
Quindi calcoliamo come segue: 199,96/0,8229, da cui otteniamo 243.
Quindi: 1/243, da cui otteniamo 0,00411.
Questo sarà il valore della 1X1.
Otteniamo quindi il seguente quadrato, su time frame mensile, pienamente gestibile.
I segni rossi al suo interno indicano setup temporali e statici e dinamici di prezzo, in corrispondenza di punti di svolta.
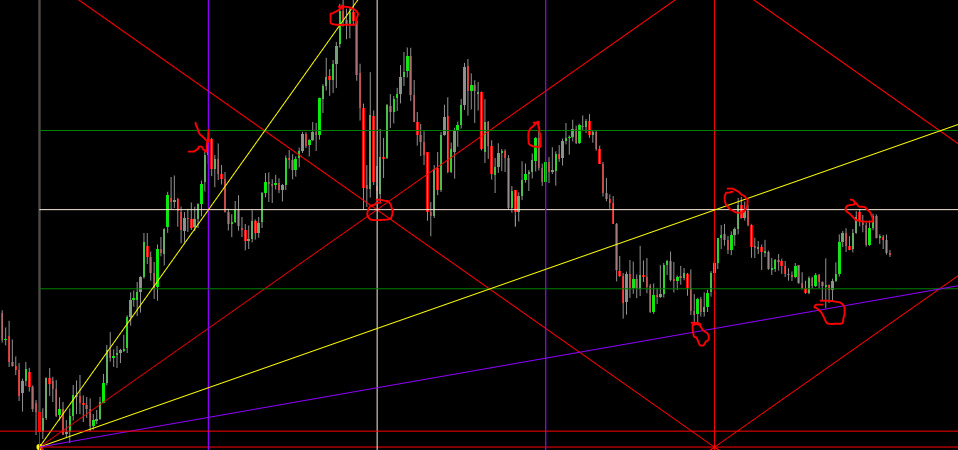
Esempio di quadrato di massimo
La stessa tecnica può essere utilizzata nella costruzione di quadrati di massimo.
Nell’esempio che segue, partiamo dal massimo a 1,6036 di ottobre 2008.
Scegliendo sempre il coefficiente 3 arriviamo (salto i passaggi intermedi) a 389,67, numero di unità temporali.
Quindi: 389,67/1,6036 porta a 243.
Quindi 1/243 porta a 0,00411, che rappresenta a il valore della nostra 1X1.
Utilizzando questi valori, otteniamo quindi il seguente grafico.
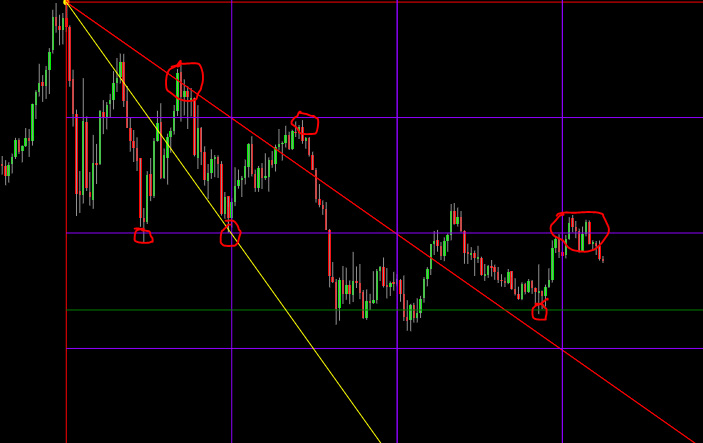
Anche per questo quadrato i segni rossi indicano riferimenti di prezzo e tempo, che individuano punti di svolta nel trend.
A cura di Gian Piero Turletti, autore di “Magic Box” e “PLT“




